《模型检验理论》阅读笔记

1. 模型检验概述

面临的问题：代码缺陷总是不可避免，但代码缺陷往往会带来灾难性的后果。

模型检验的作用：使用计算机自动寻找软硬件代码缺陷。

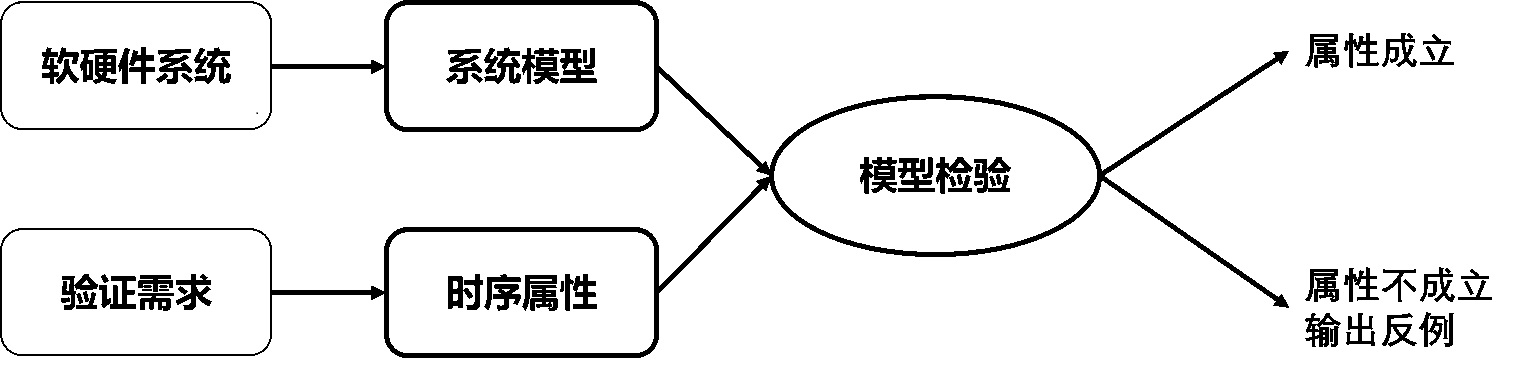
模型检验方法可以分为以下三个部分：

• 建模
• 规约
• 算法

图1 模型检验过程

2. 系统行为建模

        为实现自动验证，需要有一种支持推理的模型来对系统行为建模。迁移系统（Transition systems）是表示程序的一种标准模型，其本质是标记图（labeled graphs），其中标记可以是在节点或者边上。目前有很多迁移系统的各种不同变种。这里主要介绍Kripke结构、公平离散系统、以及Büchi自动机。

2.1 Kripke结构

        Kripke结构是模型检验中表示迁移系统的一种最流行的结构之一。Kripke结构是一个有向图，该图中的每个节点都用一些原子命题标记。该图中的节点和边分别称为“状态”和“迁移”。该结构的本质是状态标记迁移系统

1. 定义1（Kripke结构）

用五元组K=〈AP,S,S₀,R,L〉来表示一个Kripke结构，其中：

• AP是一个有限的原子命题集合
• S是一个有限的状态集合
• S₀表初始状态集合(S₀⊆S)
• R表示迁移关系
• L是一个标记函数，标记每一个状态上成立的原子命题。例L(s)表示在状态s上成立的原子命题集合。

例子：电梯运行问题的Kripke结构

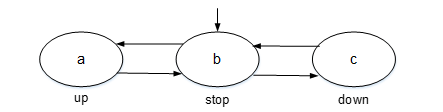
• AP={a, b, c}，其中a, b, c是三个原子命题，分别表示电梯往上运行、电梯停止和电梯往下运行
• S={up, stop, down}
• S₀={stop}
• R={(stop, up),(up, stop),(stop, down),(down, stop)}
• L(stop)={b}, L(up)={a}, L(down)={c}，分别表示在stop状态中电梯停止，在up状态中电梯往上运行，在down状态中电梯往下运行。

2. 定义2（路径）

        一条路径（Path）是指从某个状态s∈S出发的一条最长的状态序列σ=s₀,s₁,s₂⋯，其中s₀ = s，并且对任意的i ≥ 0，有(s_i, s_i+1)∈R。 σ是一个最长的状态序列是指𝜎包含无限个状态，或者𝜎的最后一个状态没有后继状态。

3. 定义3（执行）

给定一个Kripke结构K=〈AP, S, S₀, R, L〉，一个执行（Run）是指从某个初始状态s₀∈S₀出发的一条路径σ。

        基于离散状态变化的相关模型有时也被称为自动机（automata）、状态机（state machines）、状态图（state diagrams）、标记迁移系统（labeled transition systems）等。在很多情况下，一个检测算法很容易在这些模型之间进行移植。

3. 模型检验算法

3.1 显示状态模型检验

显示状态模型检验（Explicit-State Model Checking）是最早的模型检验算法之一。

• 它显示地枚举系统的每一个状态或路径，判断属性是否在每一个状态或每一条路径上都成立
• 特别适合于软件的验证，尤其是异步软件系统的验证
• 在显示状态模型检验中可以使用抽象（abstract）技术和偏序规约技术（Partial Order Reduction）进行剪枝，显著的减少其搜索空间
• 可用于安全属性和活性属性的验证

显示状态模型检验需要满足的几个条件：

1. 待验证系统必须是有限状态的
2. 可以将系统执行建模为一系列独立的状态转换

        下面以可达性分析算法为例，介绍基本的显示状态模型检验方法。基本的可达性分析算法可以实现为深度优先搜索算法或宽度优先搜索算法。该算法从系统的初始状态开始，对系统的所有可达状态进行搜索。

3.2 基于约束求解的模型检验